Gini Coefficient

To assess the reliability of potential borrowers, lending organizations use credit scoring models. These are statistical models that generate a consumer’s credit score based on various data about their financial behavior.

The issue is that not all credit scoring models demonstrate high objectivity. For the lender, it is important to know that the credit score can be relied upon when deciding on issuing a loan.

Therefore, lending organizations use various metrics to assess credit scoring models' predictive power. One of them is the Gini coefficient, also known as the Gini coefficient index or Gini Ratio.

‍

Definition of Gini coefficient​

The Gini coefficient is a measure of discriminatory power, which in the context of risk assessment helps determine how objectively a scoring model distinguishes “good” borrowers from “bad” ones. 

In other words, it helps identify those who are highly likely to fulfill their obligations under a loan agreement from potential defaulters.

The relationship between the Gini coefficient and the model's discriminatory power is as follows:

• A higher coefficient indicates a better ability of the model to predict creditworthiness.
• A lower coefficient points to a weak discriminatory ability of the scoring model.

‍

Range of Gini coefficient

What is the Gini coefficient range? This coefficient is expressed as a numerical value from 0 to 1. 

Here, 0 means no discriminatory power. Roughly speaking, such a scoring model produces results no better than random selection.

While 1 indicates perfect predictive power. That is, the credit scoring model very accurately distinguishes between reliable borrowers and defaulters.

It is worth noting that a value of 1 is rarely encountered in the real world. In practice, for digital credit scoring, typical Gini coefficient values range from 0.5 to 0.7. The latter indicates a high level of model effectiveness.

‍

Calculation of Gini coefficient

There are several ways to calculate the Gini coefficient. The most common method is as follows:

1. A credit score is generated for each potential borrower.
2. All applicants are ranked by the likelihood of repaying the loan.
3. The coefficient is calculated by comparing positive and negative results.

‍

Relationship between Gini coefficient and Area Under the Curve

How to calculate the Gini coefficient mathematically? For this, there is a Gini coefficient formula, which also uses another metric of discriminatory power in scoring models – Area Under the Curve (AUC).

AUC helps calculate the probability that the model will correctly classify reliable and unreliable borrowers.

This formula looks like this:

G (Gini coefficient) = 2×AUC−1 

Thanks to its close connection with AUC, the Gini Ratio allows for a quick and accurate understanding of a scoring model's ability to distinguish between creditworthy borrowers and defaulters.

‍

Use of the Gini coefficient in credit scoring

The Gini coefficient index helps optimize credit scoring for online lenders. It is used for the following purposes:

1. Evaluation of the scoring model. Credit scoring models assign a credit score to potential borrowers, ranking them from the highest to the lowest predicted creditworthiness.

The Gini coefficient helps determine how accurate this ranking is.

2. Comparison of multiple models. This coefficient can be used to compare the discriminatory power of several models and choose the one with the higher score.

3. Risk management. Choosing a model with a higher Gini Ratio allows lenders to make well-founded lending decisions. This helps reduce loan defaults, thereby increasing business profitability.

‍

Improving the Gini coefficient with alternative data

Traditional scoring models, such as FICO, rely on financial information about consumers – their credit history.

This approach to assessing creditworthiness has its drawbacks. These include questionable relevance of such data, one-sided evaluation of consumers, and significant opportunities for data manipulation.

All of this leads to a decrease in the discriminatory power of scoring models, that is, low Gini coefficient values.

To improve this, lenders are increasingly turning to alternative data providers. They enrich credit scoring models with non-traditional data, with digital footprints of internet users being among the most informative.

This is all the information that remains online as a result of their online activity, namely:

• Activities on social networks
• Email address information
• Information from mobile operators
• Subscriptions to paid services
• Purchases on e-commerce platforms
• Registrations on various resources

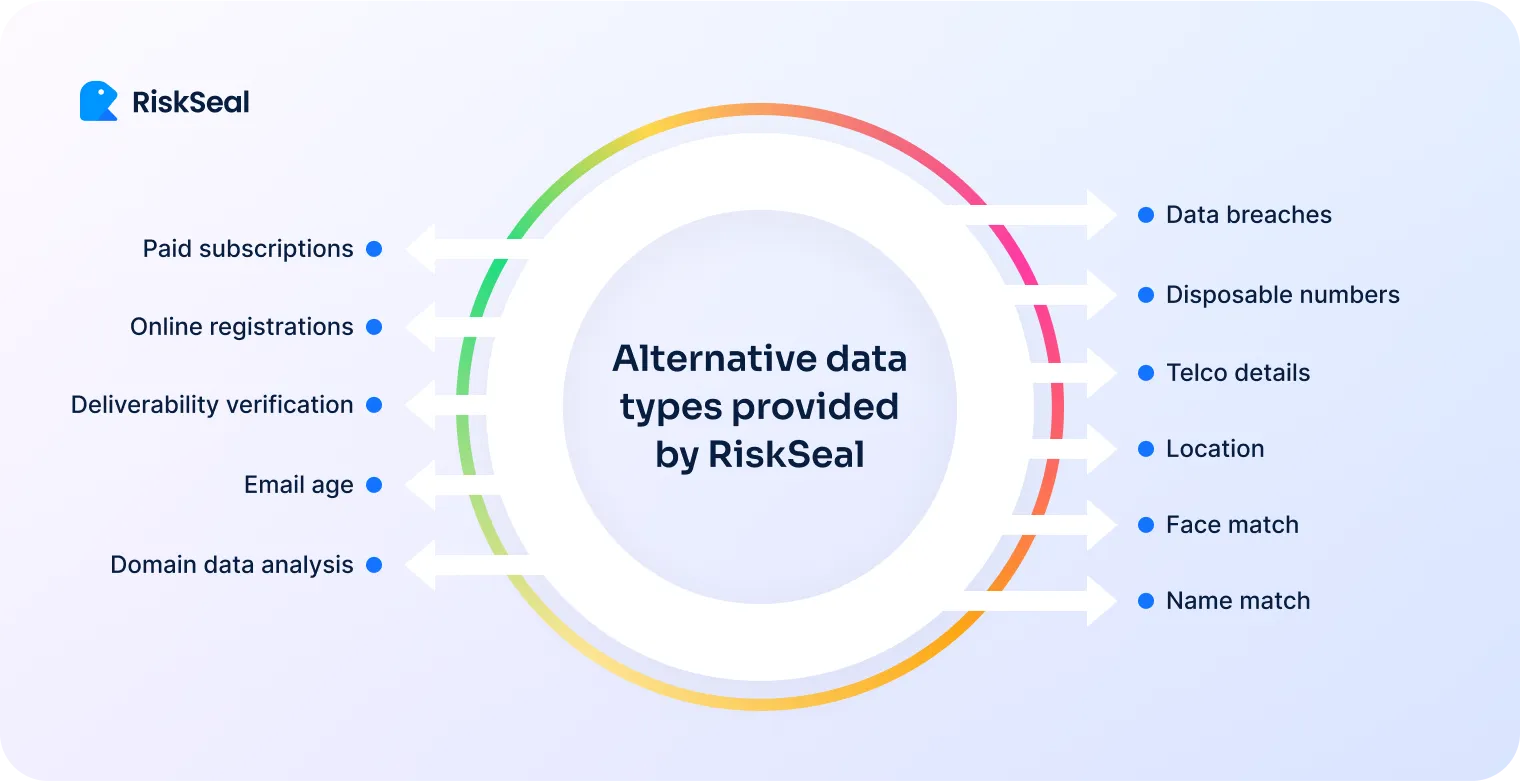
This step positively impacts the predictive power of the model and, accordingly, increases the Gini coefficient.

‍

Related Articles

How to Assess the Effectiveness of Credit Scoring Models

Identity Verification - Tree Advanced Borrowers' Checks

Economic Benefits of Enhanced Scoring Models

‍